String processing.

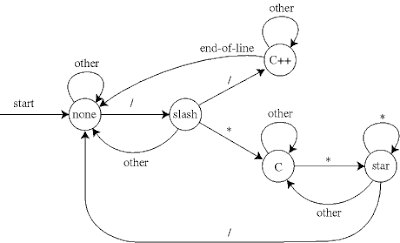
String processing. The program CommentStripper.java reads in a Java (or C++) program from standard input, removes all comments, and prints the result to standard output. This would be useful as part of a Java compiler. It removes /* */ and // style comments using a 5 state finite state automaton. It is meant to illustrate the power of DFAs, but to properly strip Java comments, you would need a few more states to handle extra cases, e.g., quoted string literals like s = "/***//*". The picture below is courtesy of David Eppstein.

DEFINATION & DESCRIPTION OF Finite state automata.

Finite state automata. A deterministic finite state automaton (DFA) is, perhaps, the simplest type of machine that is still interesting to study. Many of its important properties carry over to more complicated machines. So, before we hope to understand these more complicated machines, we first study DFAs. However, it is an enormously useful practical abstraction because DFAs still retain sufficient flexibility to perform interesting tasks, yet the hardware requirements for building them are relatively minimal. DFAs are widely used in text editors for pattern matching, in compilers for lexical analysis, in web browsers for html parsing, and in operating systems for graphical user interfaces. They also serve as the control unit in many physical systems including: vending machines, elevators, automatic traffic signals, and computer microprocessors. Also network protocol stacks and old VCR clocks. They also play a key role in natural language processing and machine learning.

A DFA captures the basic elements of an abstract machine: it reads in a string, and depending on the input and the way the machine was designed, it outputs true or false. A DFA is always is one of N states, which we name 0 through N-1. Each state is labeled true or false. The DFA begins in a distinguished state called the start state. As the input characters are read in one at a time, the DFA changes from one state to another in a prespecified way. The new state is completely determined by the current state and the character just read in. When the input is exhausted, the DFA outputs true or false according to the label of the state it is currently in.

UPPER PICTURE is an example of a DFA that accepts binary strings that are multiples of 3. For example, the machine rejects 1101 since 1101 in binary is 13 in decimal, which is not divisible by 3. On the other hand, the machine accepts 1100 since it is 12 in decimal.

Abstract machines

Abstract machines. Modern computers are capable of performing a wide variety of computations. An abstract machine reads in an input string, and, depending on the input, outputs true (accept), outputs false (reject), or gets stuck in an infinite loop and outputs nothing. We say that a machine recognizes a particular language, if it outputs true for any input string in the language and false otherwise. The artificial restriction to such decision problems is purely for notational convenience. Virtually all computational problems can be recast as language recognition problems. For example, to determine whether an integer 97 is prime, we can ask whether 97 is in the language consisting of all primes {2, 3, 5, 7, 13, ... } or to determine the decimal expansion of the mathematical constant π we can ask whether 7 is the 100th digit of π and so on.

We would like to be able to formally compare different classes of abstract machines in order to address questions like Is a Mac more powerful than a PC? Can Java do more things than C++? To accomplish this, we define a notion of power. We say that machine A is at least as powerful as machine B if machine A can be "programmed'" to recognize all of the languages that B can. Machine A is more powerful than B, if in addition, it can be programmed to recognize at least one additional language. Two machines are equivalent if they can be programmed to recognize precisely the same set of languages. Using this definition of power, we will classify several fundamental machines. Naturally, we are interested in designing the most powerful computer, i.e., the one that can solve the widest range of language recognition problems. Note that our notion of power does not say anything about how fast a computation can be done. Instead, it reflects a more fundamental notion of whether or not it is even possible to perform some computation in a finite number of steps.

DEFNATION OF Turing machines

Turing machines are the most general automata. They consist of a finite set of states and an infinite tape which contains the input and is used to read and write symbols during the computation. Since Turing machines can leave symbols on their tape at the end of the computation, they can be viewed as computing functions: the partial recursive functions. Despite the simplicity of these automata, any algorithm that can be implemented on a computer can be modeled by some Turing machine.

Turing machines are used in the characterization of the complexity of problems. The complexity of a problem is determined by the efficiency of the best algorithm that solves it. Measures of an algorithm's efficiency are the amount of time or space that a Turing machine requires to implement the algorithm. A computation's time is the number of configurations involved in that computation, and its space corresponds to the number of positions on its tape that were used.

DEFINATION ABOUT Automata Theory

Automata theory is a further step in abstracting your attention away from any
particular kind of computer or particular programming language. In automata theory
we consider a mathematical model of computing. Such a model strips the computational
machinery—the “programming language”—down to the bare minimum, so that it’s easy
to manipulate these theoretical machines (there are several such models, for different purposes, as you’ll soon see) mathematically to prove things about their capabilities.
For the most part, these mathematical models are not used for practical programming
problems. Real programming languages are much more convenient to use. But the very
flexibility that makes real languages easier to use also makes them harder to talk about in a formal way. The stripped-down theoretical machines are designed to be examined

mathematically.

What’s a mathematical model? You’ll see one shortly, called a “finite-state machine.”
The point of this study is that the mathematical models are, in some important ways,
to real computers and real programming languages. What this means is that
any problem that can be solved on a real computer can be solved using these models,and vice versa. Anything we can prove about the models sheds light on the real problems of computer programming as well.
The questions asked in automata theory include these: Are there any problems that
no computer can solve, no matter how much time and memory it has? Is it possible to
PROVE that a particular computer program will actually solve a particular problem? If a computer can use two different external storage devices (disks or tapes) at the same time,does that extend the range of problems it can solve compared to a machine with only one such device?
There is also a larger question lurking in the background of automata theory: Does
the human mind solve problems in the same way that a computer does? Are people
subject to the same limitations as computers? Automata theory does not actually answer this question, but the insights of automata theory can be helpful in trying to work out an answer. We’ll have more to say about this in the chapter on artificial intelligence